Y axis) Reflection over line y=x or y=Reflection over line y=x or y=xx Reflection over y=x Point (x,y) reflects to point (y,x) Reflection over line y=xThis video explains to graph graph reflections across the xaxis and yaxis in the form a*f(b(xc))d This video looks at how the sign of a and b affect thIt makes sense but at he same time it doesn't because when I pump the reflected

Learn About Reflection Over The Line Y X Caddell Prep Online
Reflection over x and y axis equation
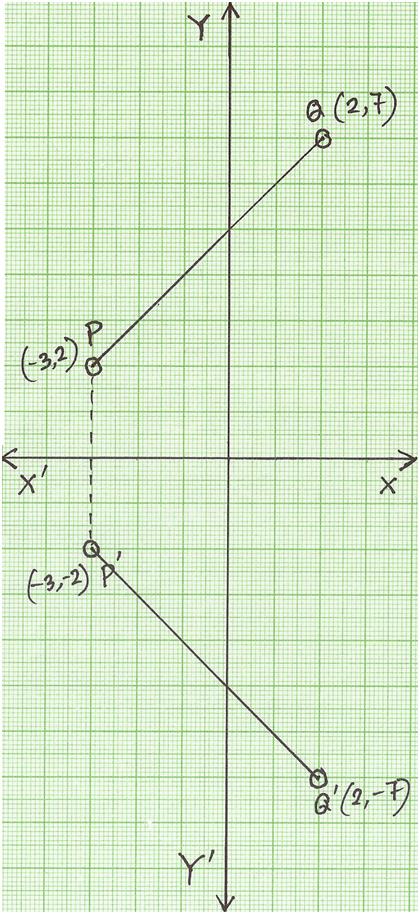
Reflection over x and y axis equation-When we multiply the parent function f (x) = bx f (x) = b x by –1, we get a reflection about the x axis When we multiply the input by –1, we get a reflection about the y axis For example, if we begin by graphing the parent function f (x) = 2x f (x) = 2 The rule for reflecting over the X axis is to negate the value of the ycoordinate of each point, but leave the xvalue the same For example, when point P with coordinates (5,4) is reflecting across the X axis and mapped onto point P', the coordinates of P' are (5,4)




Lesson Worksheet Function Transformations Reflection Nagwa
Reflection in the x axis A reflection of a point over the x axis is shown The rule for a reflection over the x axis is ( x , y ) → ( x , − y ) Reflection in the y axis A reflection of a point over the y axisA function f f is called an even function if f(x)= f(−x) f ( x) = f ( − x) for all x x in the domain of f f In other words, a function is even if performing a reflection about the y y axis does not change the graph of the function To help remember the definition of an even function, notice that the example of an even function we gaveThe equation of the line of symmetry To describe a reflection on a grid, the equation of the mirror line is needed Example Reflect the shape in the line \(x = 1\) The line \(x = 1\) is a
Reflections Lesson covers reflections over four quadrants Learners initially identify the equation of the vertical and horizontal lines Learners then identify how to reflect a shape in the x or y axis Lesson is consolidated with a plenary which can take place using miniwhiteboards or as a discussion The lesson doesn't cover y = xApply the rule to find the vertices of the image Since there is a reflection across the xaxis, we have to multiply each ycoordinate by 1 That is, (x, y) > (x, y) Step 2Reflections in Math Applet Interactive Reflections in Math Explorer Demonstration of how to reflect a point, line or triangle over the xaxis, yaxis, or any line x axis y axis y = x y = x Equation Point Segment Triangle Rectangle y =
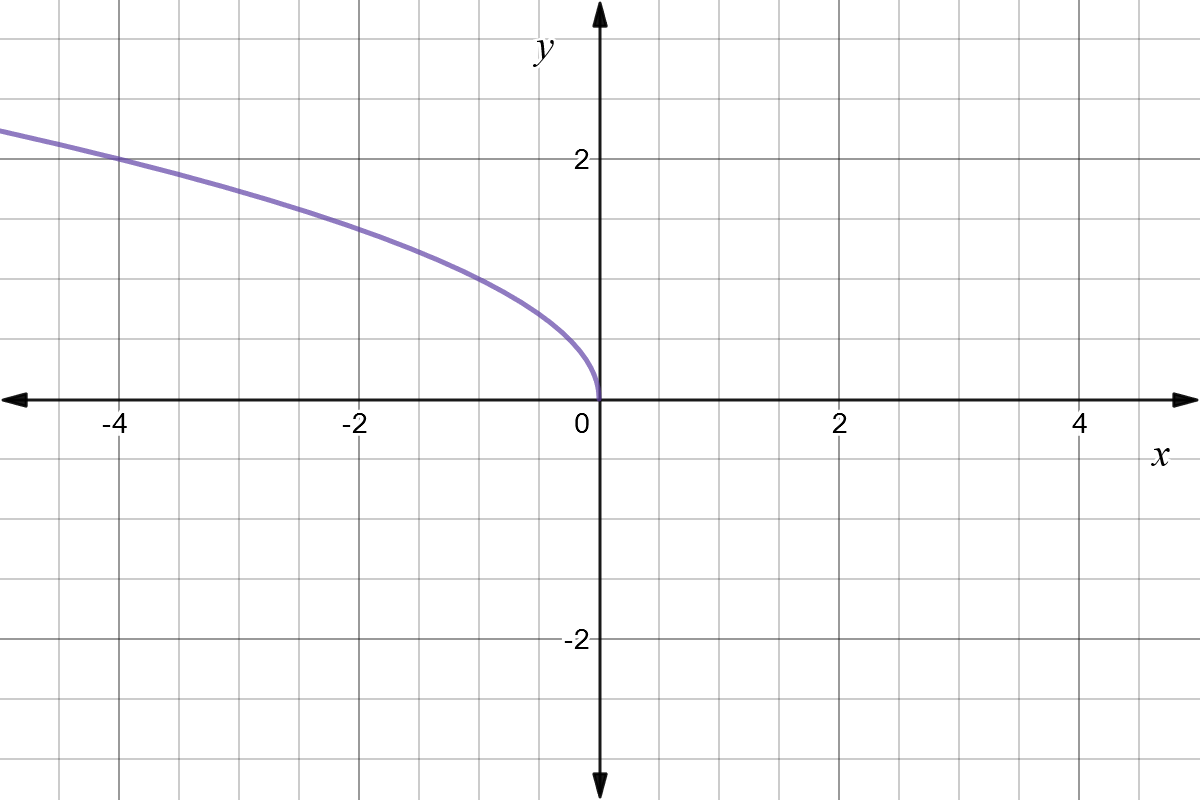
Reflection over the line y = − x A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the y = − x (A, B) → (− B, − A)Let y = f (x) be a function In the above function, if we want to do reflection through the yaxis, x has to be replaced by x and we get the new function y = f (x) The graph of y = f (x) can be obtained by reflecting the graph of y = f (x) through the yaxis The notation or rule for a reflection over the yaxis is (x, y) → (x, y)



Solution Starting With The Graph Of Y E X Find The Equation Of The Graph That Results From Reflecting About The Line Y 5



Ch 3 4
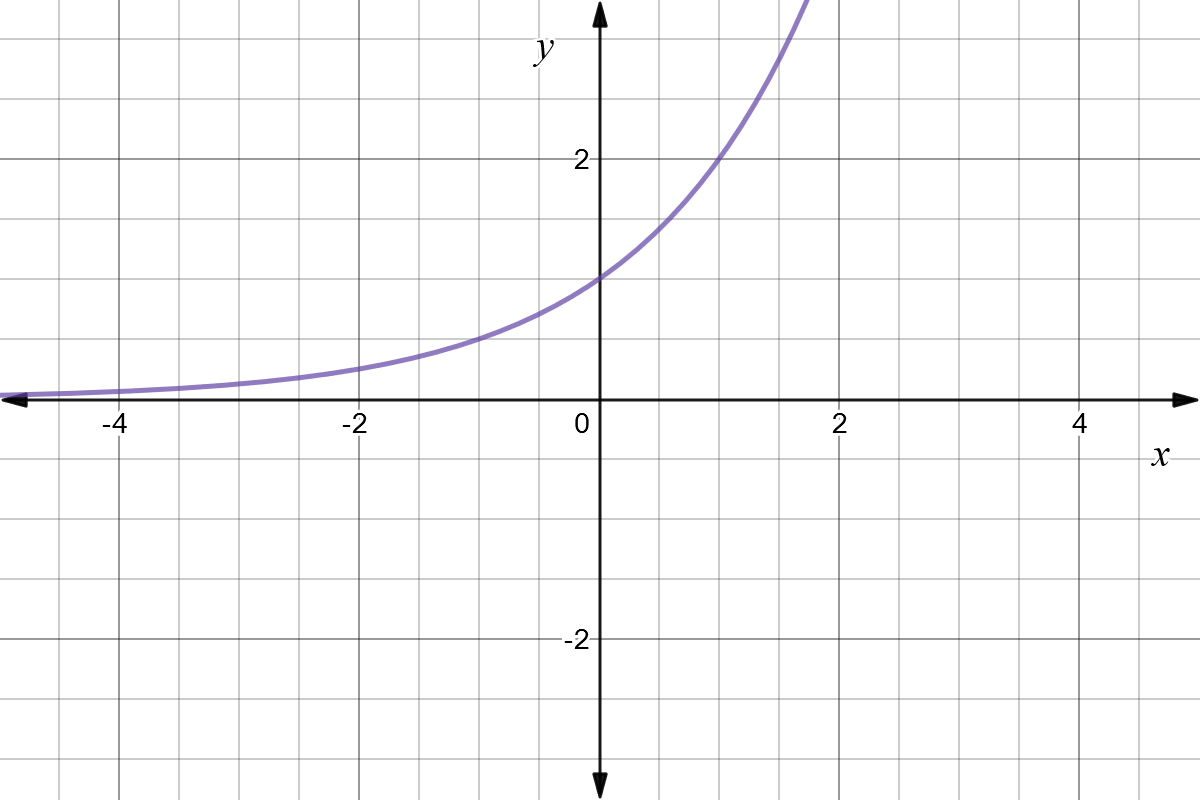
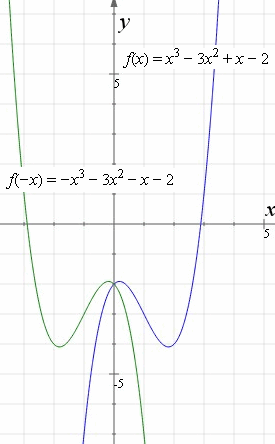
👉 Learn how to graph exponential functions in base e An exponential function is a function whose value increases rapidly e is a constant called the exponeAnswer In Exercises 29 − 32, find the equation of the reflection of f across (a) the x axis and (b) the y axis f ( x) = x 3 − 5 x 2 − 3 x 2 Precalculus Graphical, Numerical, Algebraic Chapter 1 Functions and GraphsSummary Reflections and Rotations Reflections and Rotations We can also reflect the graph of a function over the xaxis (y = 0), the yaxis(x = 0), or the line y = x Making the output negative reflects the graph over the xaxis, or the line y = 0 Here are the graphs of y = f (x) and y = f (x)




The Graph Shown To The Right Involves A Reflection In Chegg Com



Search Q Vertical Compression Tbm Isch
Dilations make the graph wider or thinner Reflections flip the graph like a mirror In the standard form absolute value equation, y=axhk, hPurplemath The last two easy transformations involve flipping functions upside down (flipping them around the xaxis), and mirroring them in the yaxis The first, flipping upside down, is found by taking the negative of the original function;The equation of the line of the mirror line To describe a reflection on a grid, the equation of the mirror line is needed Example Reflect the shape in the line \(x = 1\) The line \(x = 1



Reflection Of A Point In X Axis Reflection Of A Point Reflection




Reflecting Functions Examples Video Khan Academy
VIEW ENTIRE PLAYLIST http//wwwyoutubecom/view_play_list?p=0D2E061AF3327C If this helps, please leave a comment and subscribe!Q) and (r, s) (In the graph below, the equation of the line of reflection is y = 2/3x 4 Note that both segments have slopes = 3/2, and the shorter segments on both sides of the line of reflection also have slopes = 3/2 If you are using a xy coordinate axes drawn with a 11 aspect ratio, you can find preimage and image points by just counting Write the equation for the final transformed graph of f after the indicated transformations are applied to its graph f(x) = 4\sqrt{x}, reflect in the yaxis




Reflection Transformation Matrix



Reflections Of A Graph Topics In Precalculus
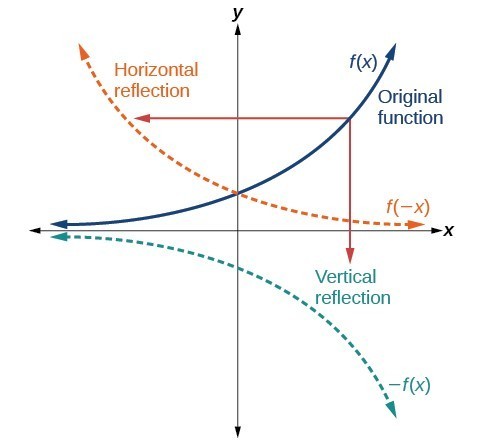
The answer from question (1) is reflected in the line x = 4 What is the equation of the image?Another transformation that can be applied to a function is a reflection over the latexx/latex– or latexy/latexaxis A vertical reflection reflects a graph vertically across the latexx/latexaxis, while a horizontal reflection reflects a graph horizontally across the latexy/latexaxis The reflections are shown in Figure 9F ( x) \displaystyle f\left (x\right) f (x), a new function g ( x) = f ( − x) \displaystyle g\left (x\right)=f\left (x\right) g(x) = f (−x) is a horizontal reflection of the function f ( x) \displaystyle f\left (x\right) f (x), sometimes called a reflection about the y axis




Scaling Reflecting Parabolas Video Khan Academy




Inverse Function Reflection In Y Axis Mathematics Stack Exchange
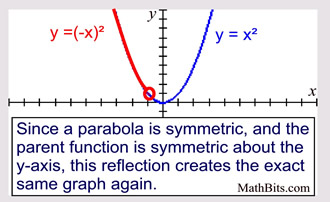
Based on the definition of reflection across the xaxis, the graph of y 1 (x) should look like the graph of f (x), reflected across the xaxis Take a look at the graphs of f ( x ) and y 1 ( x ) Function (2), g ( x ), is an absolute value functionPolar graph polar equation symmetry reflection x axis y axis symmetric about the x axis symmetric about the y axis 304 videos Symmetry of Polar Graphs Precalculus Polar Coordinates and Complex Numbers How to determine if the graph of a polar equation is symmetric about the xaxisThe graph of y=k⋅x² is the graph of y=x² scaled by a factor of k If k



Reflect Function About Y Axis F X Expii



Reflect Function About Y Axis F X Expii
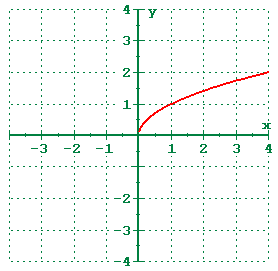
You can also negate the value depending on the line of reflection where the xvalue is negated if the reflection is over the yaxis and the yvalue is negated if the reflection is over the xaxis Either way, the answer is the same thing For example Triangle ABC with coordinate points A(1,2), B(3,5), and C(7,1)P (x) = a (x)^2 b (x) c = ax^2 bx c 11K views Reflection of the square root function over the yaxis Square Root Function Reflection of the Square Root Function across the yaxis Now, I know the domain of a square root has to be equal to or greater than zero So that's when imaginary numbers are used Right?



Section 4 3 Reflecting Graphs Symmetry Objective To Reflect Graphs And To Use Symmetry To Sketch Graphs Ppt Download



Transformations In Carnivals By Hannah Lin Joseph Choi
Use the checkboxes to investigate how the triangle is reflected in either the xaxis or the yaxis Then answer the questions below Use what you learned from the investigation above to answer the following questions 1) If the point (2, 3) is reflected over the xaxis what is the new point?The graph of y is equal to absolute value of X is reflected across the xaxis and then scaled vertically by a factor of seven what is the equation of the new graph so pause the video and see if you can figure that out alright let's work through it together now now you might not need to draw it visually but I will just so that we can all together visualize what is going on let's say that's my xAnd also, the line x = 2 (line of reflection) is the perpendicular bisector of the segment joining any point to its image Students can keep this idea in mind when they are working with lines of reflections which are neither the xaxis nor the yaxis



Reflection Objectives D Gradereflect Shapes In Lines Such As X 2 Or Y 1 Describe Reflections Fully Identify Reflection Symmetry In 3 D Solids Prior Ppt Download



Transformations Of Functions Mathbitsnotebook A1 Ccss Math
Remember that when a point P (x, y) of the coordinate plane is reflected in the y axis, it becomes the point Q (x, y) and when reflected in x axis, it becomes P' (x, y) Therefore the quadratic p (x) = ax^2 bx c (a not zero) when reflected in y axis it becomes ;The graph of y=kx is the graph of y=x scaled by a factor of k If kIt corresponds to reflecting g(x) over the yaxis Therefore, to graph h(x), we simply reflect g(x) over the yaxis by finding a few points on g(x), multiplying the xcoordinate by 1, and



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra



What Is The Reflection Over The Y Axis Of The Point 4 7 Quora
When the parent function f (x) =logb(x) f (x) = l o g b (x) is multiplied by –1, the result is a reflection about the x axis When the input is multiplied by –1, the result is a reflection about the y axisThat is, the rule for this transformation is –f (x) To see how this works, take a look at the graph of h(x) = x 2 2x – 3A vertical reflection is given by the equation latexy = f(x)/latex and results in the curve being "reflected" across the xaxis A horizontal reflection is given by the equation latexy = f(x)/latex and results in the curve being "reflected" across the yaxis Key Terms Reflection A mirror image of a function across a given line
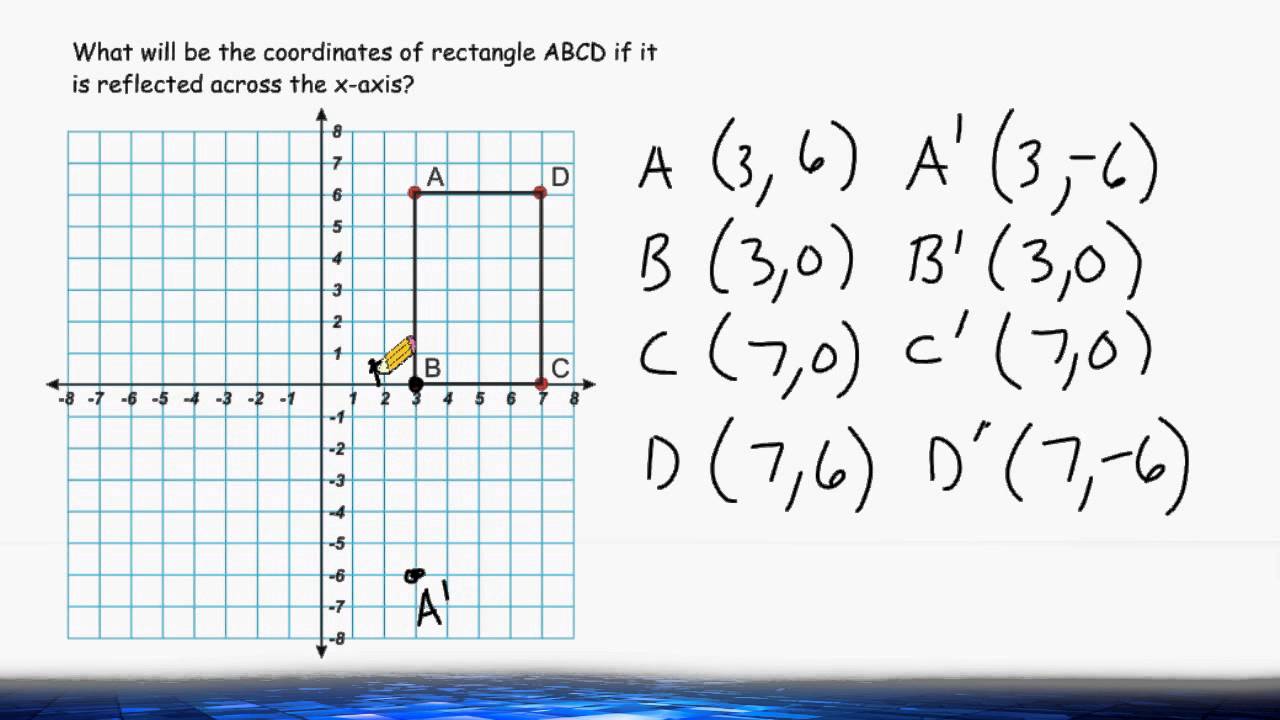



Transformations Reflection Across The X Axis Youtube
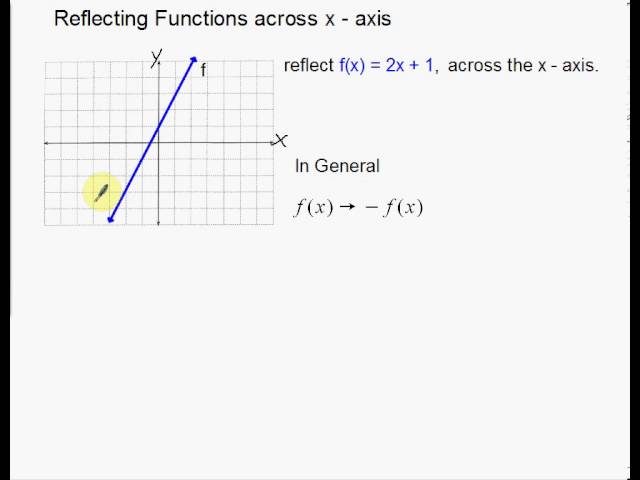



Linear Reflections Across X And Y Axis Youtube
Learn about reflection in mathematics every point is the same distance from a central line Show Ads Hide Ads A reflection is a flip over a line When the mirror line is the yaxis we change each (x,y) into (−x,y) Fold the PaperTo reflect the absolute value function over the xaxis, we simply put a negative sign before the symbol (in this case the absolute value bars) Our new equation would be y = Ix3I Check the graphs in your calculator, they should look like a mirror image of each other, reflected over the xaxis Now try reflecting reciprocal y = 1/x 4 How has the graph changed if the equation is fx21 Reflection in the x axis A 12 B 35 and C 71 By counting the units we know that point A is located two units above the xaxis Reflection over the xaxis A reflection over the xaxis can be seen in the picture below in which point A is reflected to its image A




Reflection Transformation Matrix




Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor
From the equation, you can see that the horizontal shift will be to the left 10 units and there will be a reflection over the yaxis Therefore, reflect the graph of over the yaxis and then shift (move) the reflected graph left 10 units The point (1, 0) is shifted to (1, 0) with the reflection and then to (1 10, 0) or ( 11, 0) Suppose Homogeneous Coordinate Representation We can also represent the Reflection along xaxis in the form of 3 x 3 matrix 2 Reflection along Yaxis In this kind of Reflection, the value of X is negative, and the value of Y is positive We can represent the Reflection along yaxis by following equation X1 = – X0 Y1 = Y0Polar graph polar equation symmetry reflection x axis symmetric about the x axis 303 videos Symmetry of Polar Graphs Precalculus Polar Coordinates and Complex Numbers How to determine if the graph of a polar equation is symmetric about the xaxis




R E F L E C T I O N O V E R X A X I S Zonealarm Results
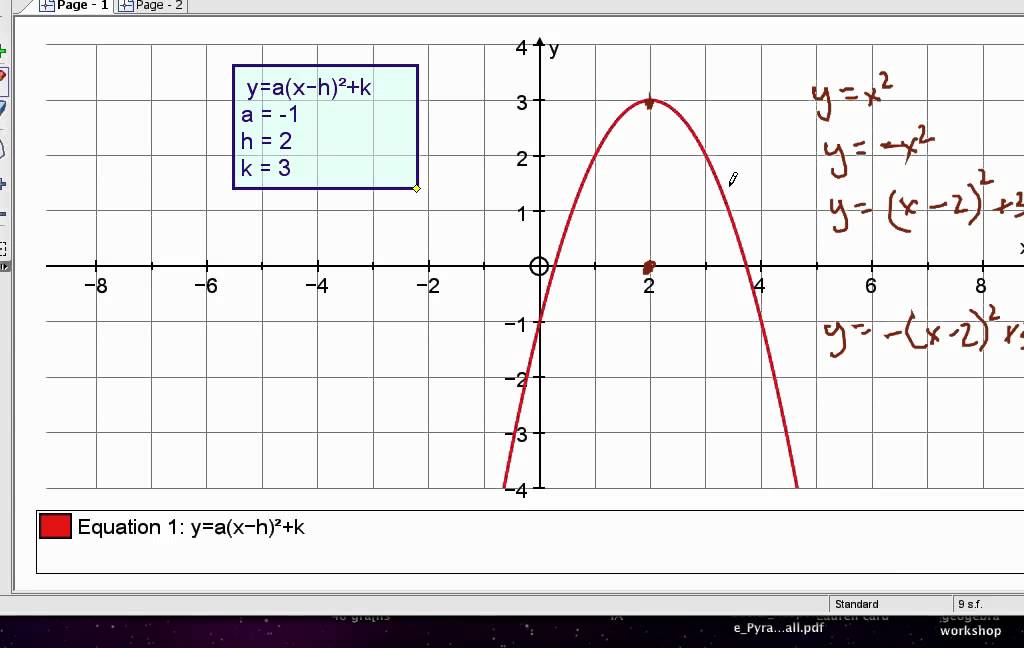



2 02 0 Reflection Over X Axis Mov Youtube
The shapes are the same The graph of is a reflection over the xaxis of the graph of Fold the graph of over the xaxis so that it would be superimposed on the graph of Every point on the graph of would be shifted up or down twice it's distance from the xaxis For example, the point (a, 8) is located 8 units up from the xaxisAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators The reflection of such a parabola over the x axis is simply written as y = (x ^2) In other words, the function of f (x) becomes f (x) when reflected over the x axis



Assignment 2 Transforming Parabolas



Solution The Line With The Equation Y 2x 3 Is Reflected In The Y Axis Find The Equation Of The Image Line
The line y = 15x – 2 is reflected in the line y = 1 What is the equation of the image?
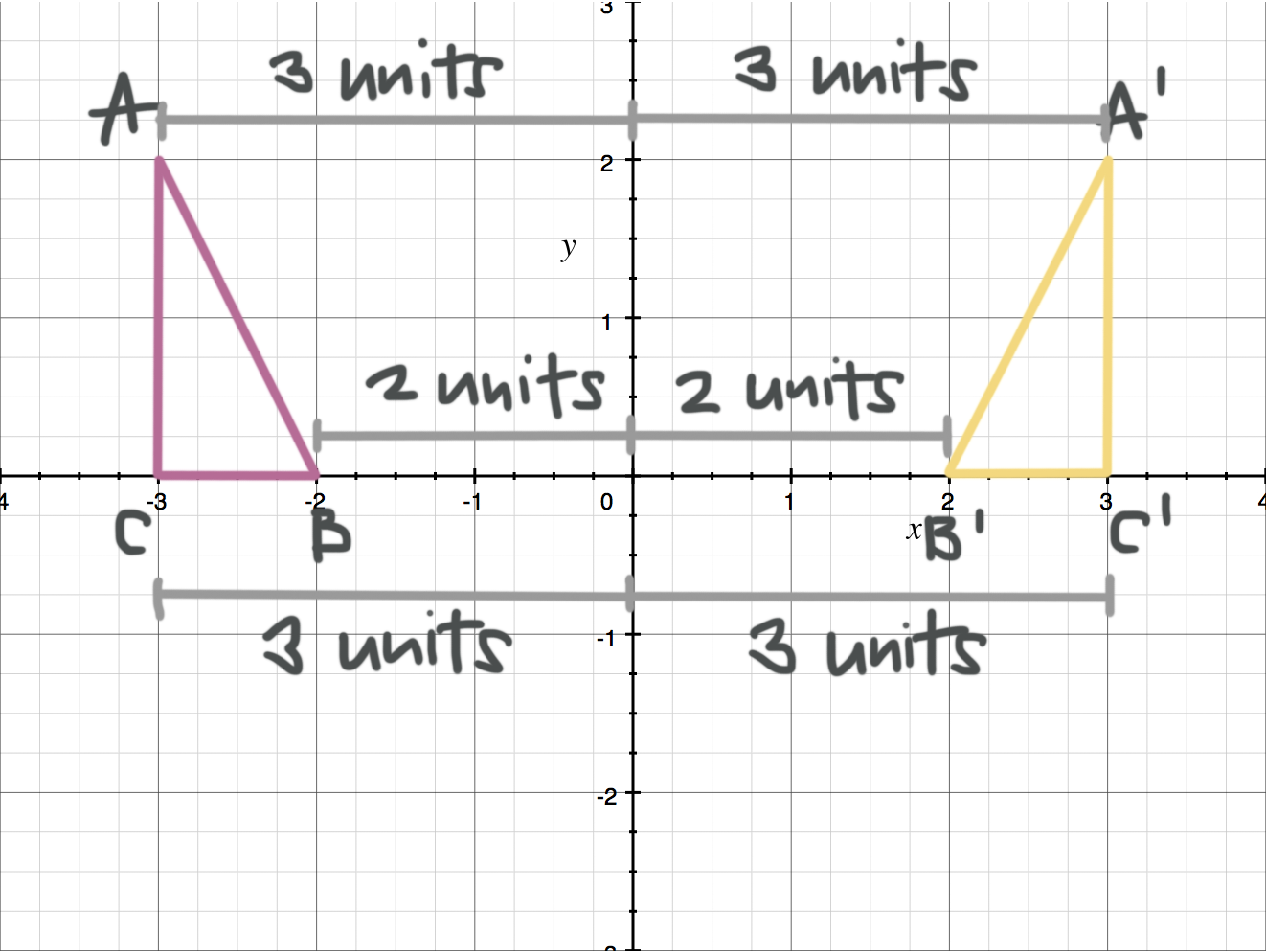



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor



How To Reflect A Graph Through The X Axis Y Axis Or Origin



1 5 Shifting Reflecting And Stretching Graphs



Parabola Parent Function Mathbitsnotebook A1 Ccss Math



Assignment 2 Transforming Parabolas



Precalculus A 4th Hour Fall 10 September 10




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation
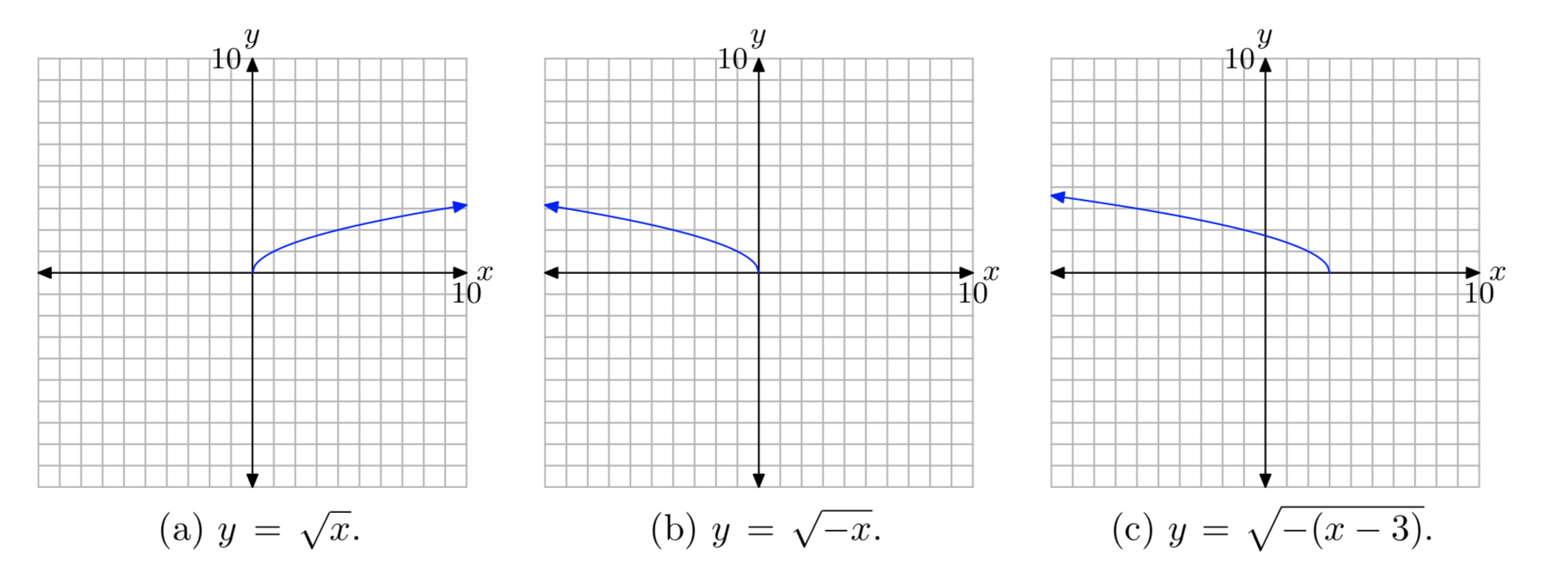



9 1 The Square Root Function Mathematics Libretexts




Reflection Over The X And Y Axis The Complete Guide Mashup Math
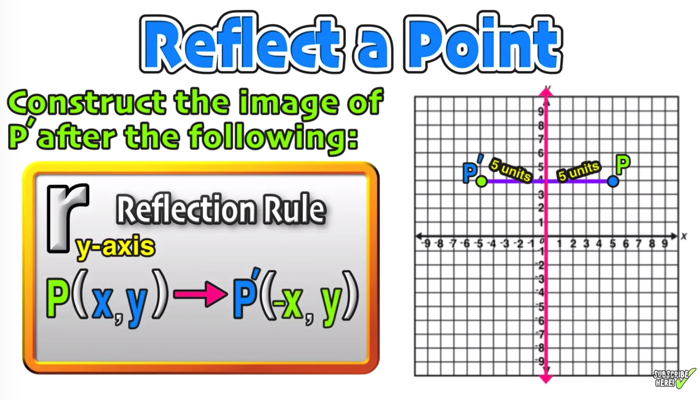



Reflection Over The X And Y Axis The Complete Guide Mashup Math




How To Reflect Quadratic Equations Video Lesson Transcript Study Com
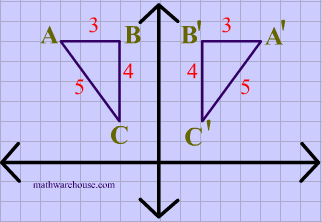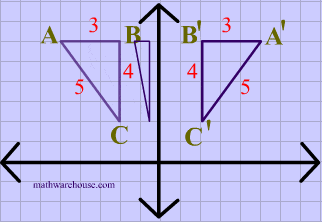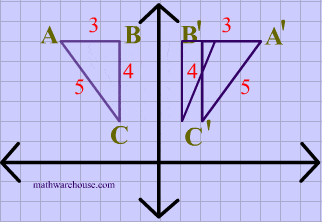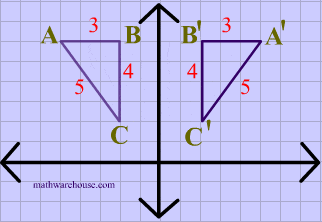



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
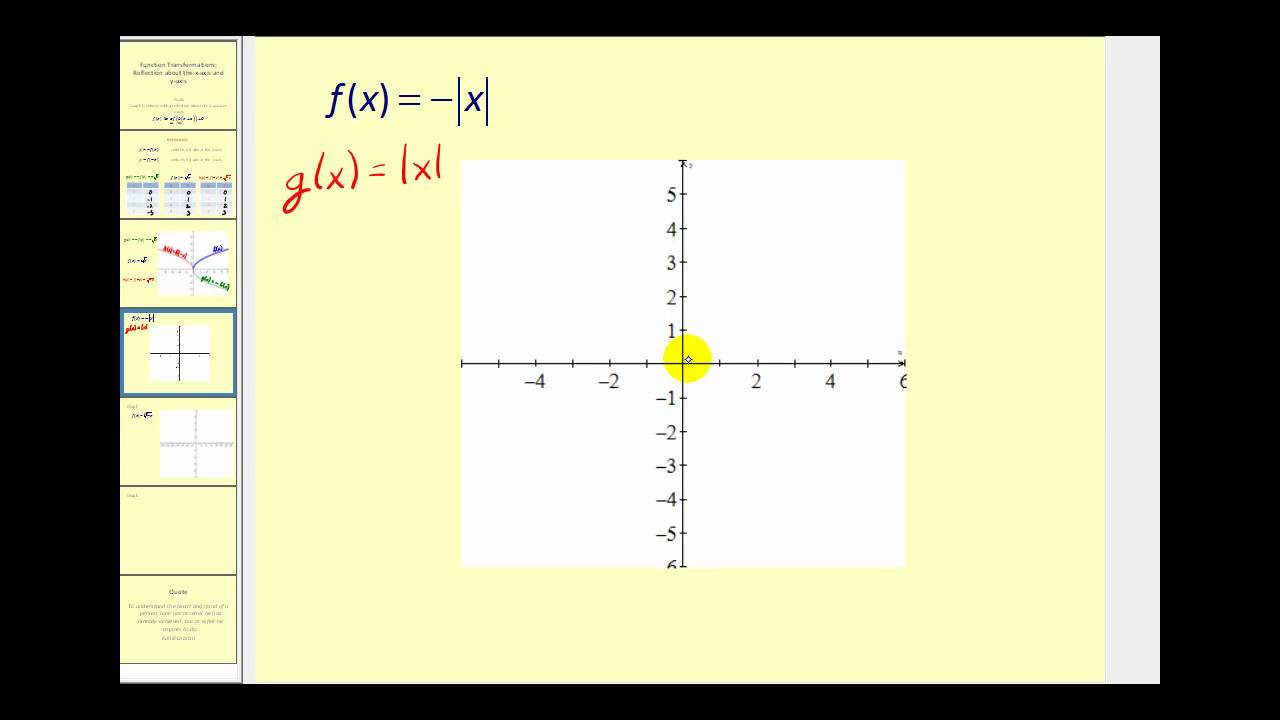



Function Transformations Reflections Across The X Axis And Y Axis Youtube




Lesson Worksheet Function Transformations Reflection Nagwa
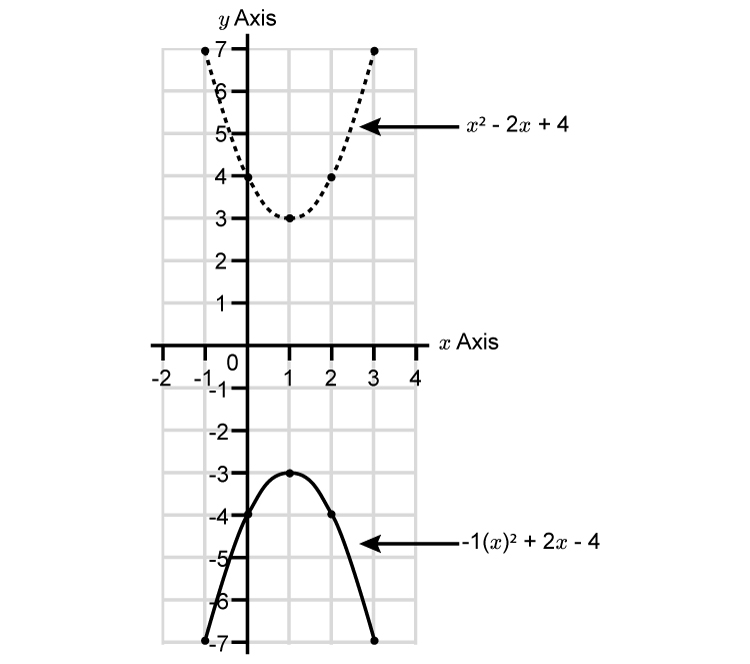



Reflecting More Difficult Parabolas Mammoth Memory Maths
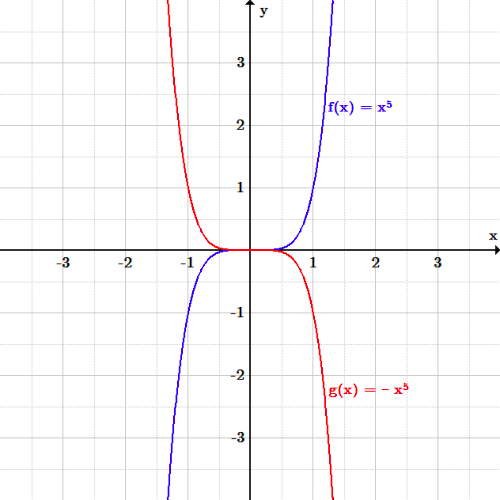



Transformations Boundless Algebra




Reflect Function About Y Axis F X Expii
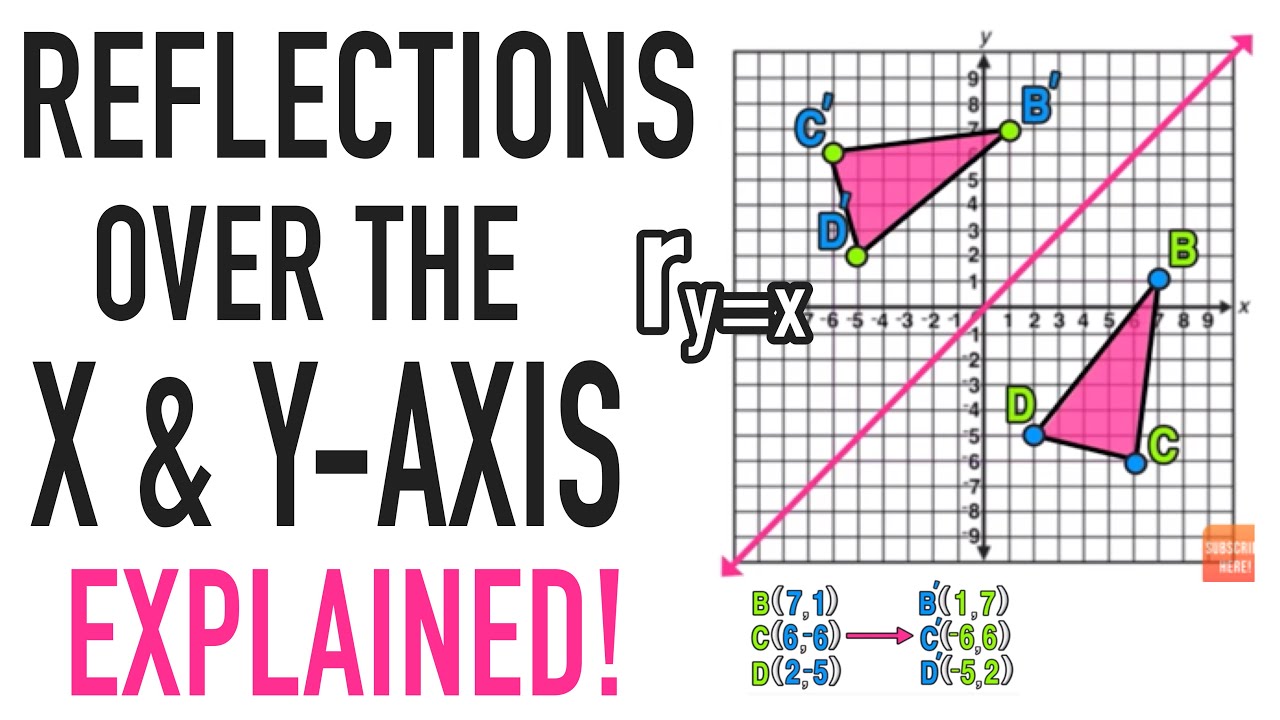



Reflections Over The X Axis And Y Axis Explained Youtube
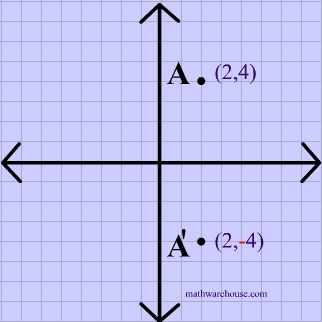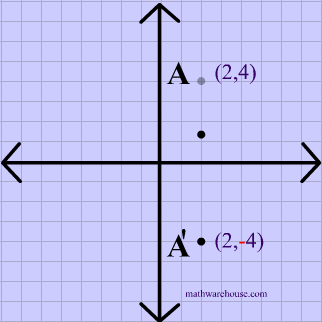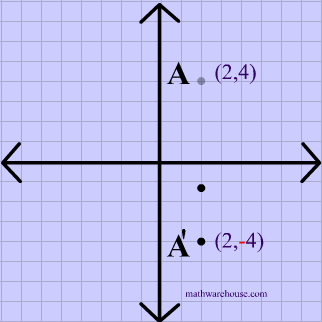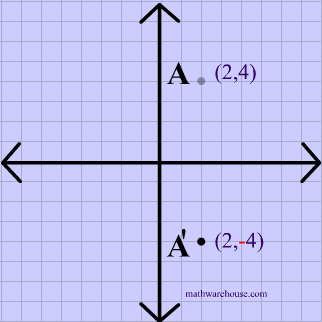



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



1
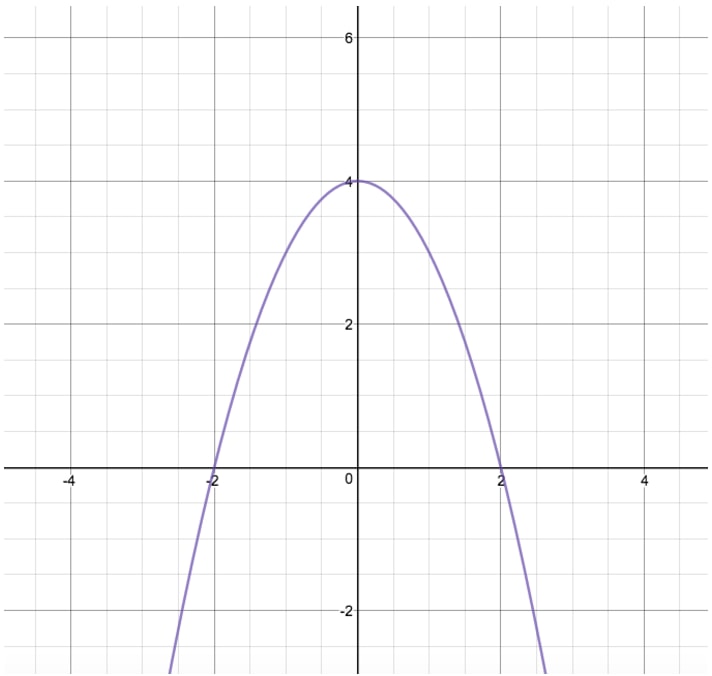



How To Reflect A Graph Through The X Axis Studypug




Cartesian Coordinate System Wikipedia
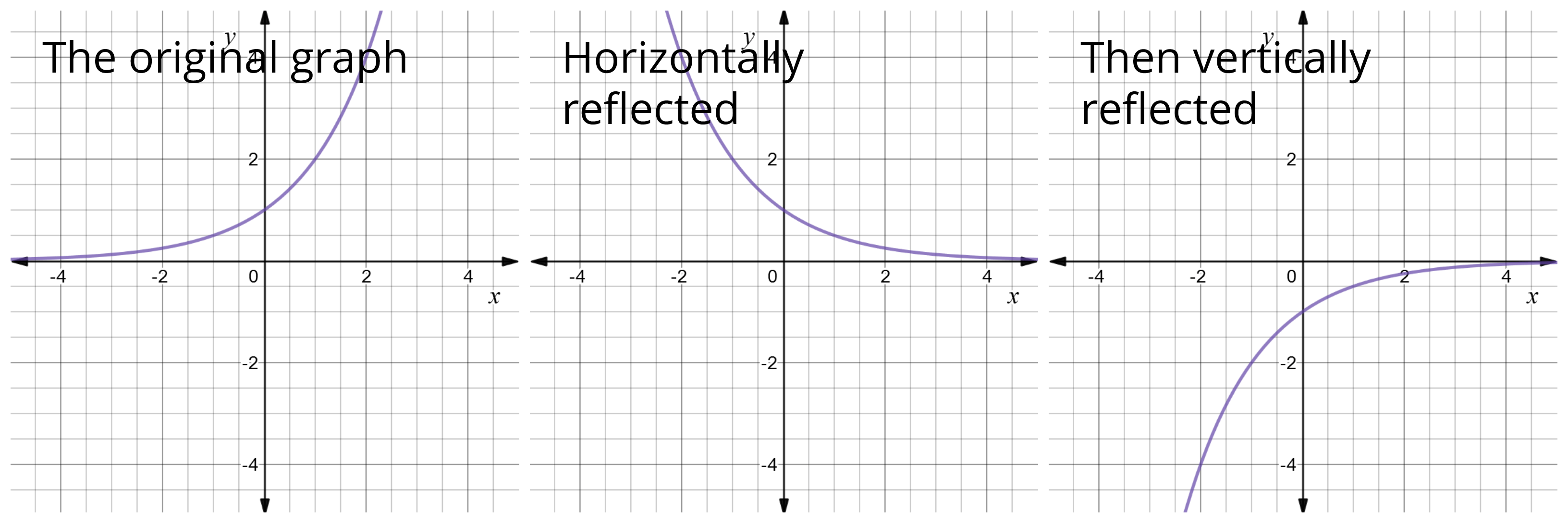



Reflect Function About Y Axis F X Expii
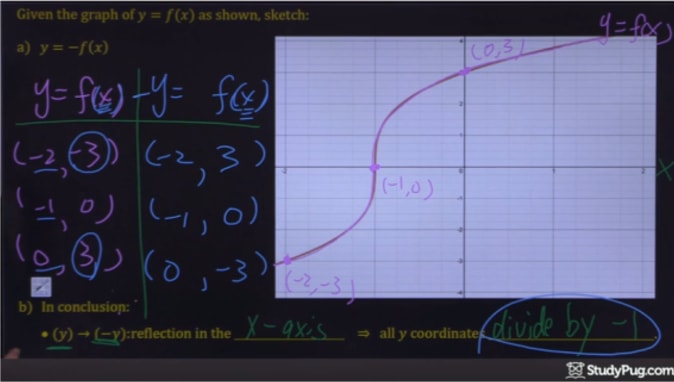



How To Reflect A Graph Through The X Axis Studypug



Assignment 2 Transforming Parabolas




Reflection Over Y X Math Geometry Showme




Reflections



Transformation Reflection Over X Axis




Reflection Rules How To W 25 Step By Step Examples




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
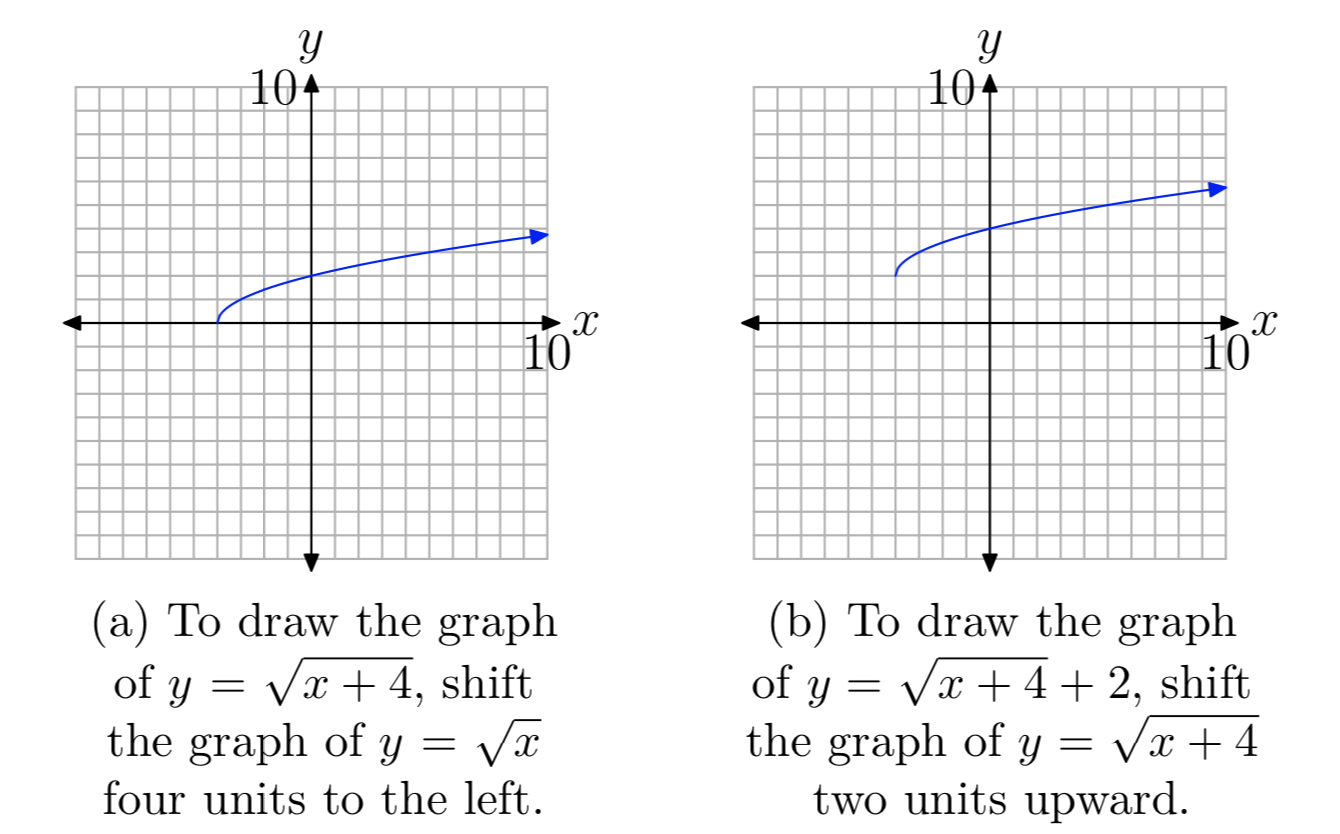



9 1 The Square Root Function Mathematics Libretexts




How To Reflect A Graph Through The X Axis Y Axis Or Origin




Transformations Boundless Algebra
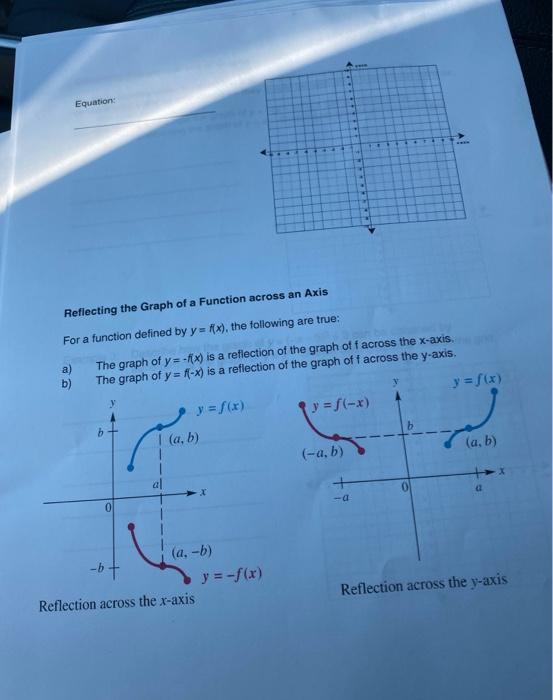



Solved Name Section 2 3 Reflecting Graphs Reflecting Acr Chegg Com




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



What Does It Mean To Reflect Over The Y X Line Quora



How To Reflect A Graph Through The X Axis Studypug
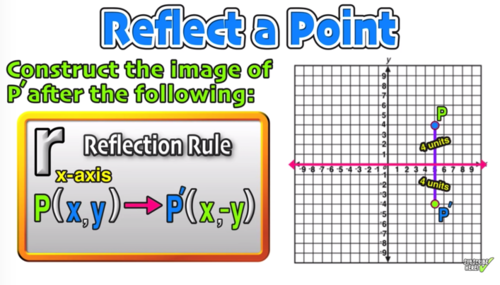



Reflection Over The X And Y Axis The Complete Guide Mashup Math



Operations On Functions Reflections And Rotations Sparknotes



Ch 3 4
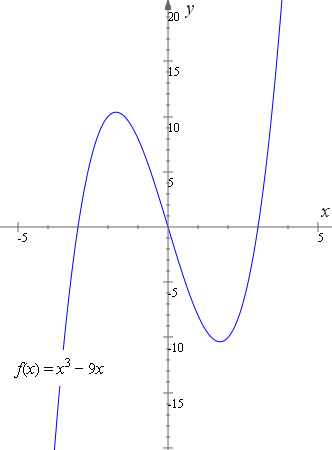



How To Reflect A Graph Through The X Axis Y Axis Or Origin




Reflection Definition Reflection In The Coordinate Plane
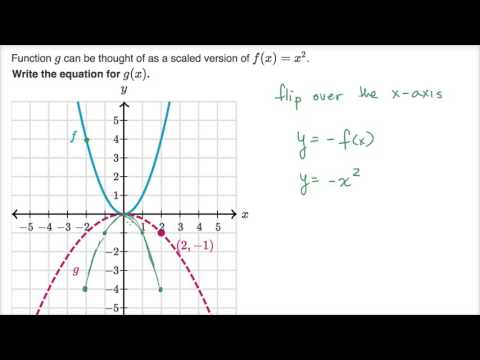



Scaling Reflecting Parabolas Video Khan Academy




Want Brainliest Get This Correct What Is The Equation Of This Function After It Is Reflected Over Brainly Com




Reflection
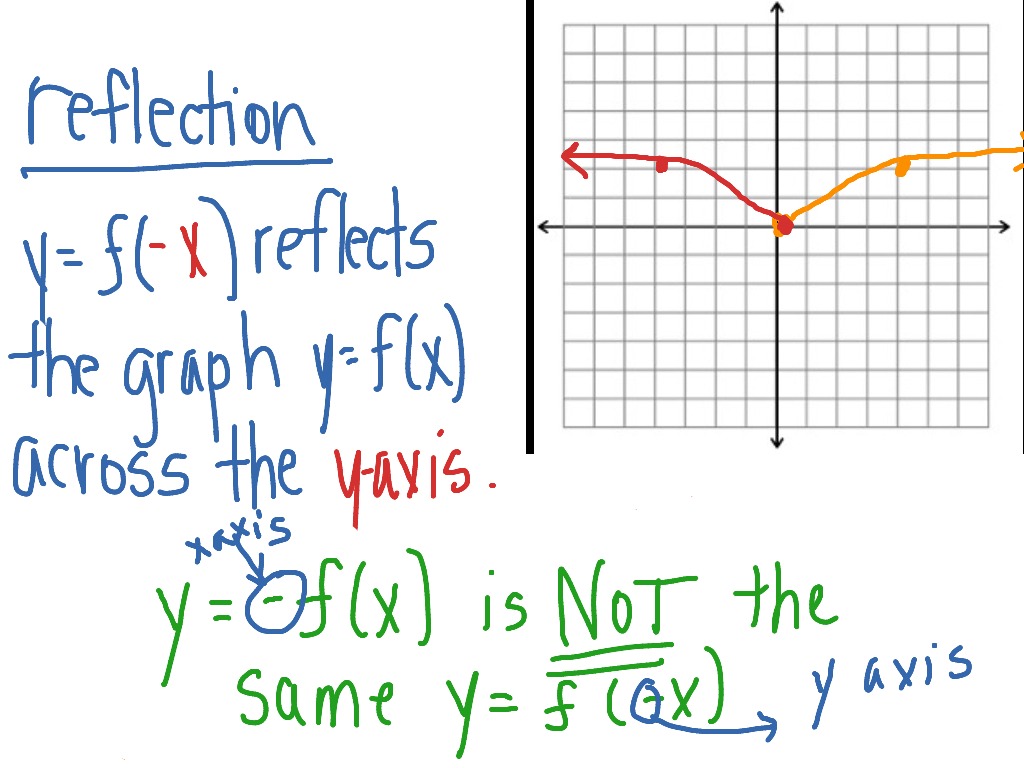



Reflection Across The Y Axis Math Functions Showme



Mbci Mb Ca Site Assets Files 1614 1 2 Pdf



1




Polar Graph Polar Equation Symmetry Reflection X Axis Symmetric About The X Axis Homework Help Videos Brightstorm



Transformations Of Functions Mathbitsnotebook A1 Ccss Math
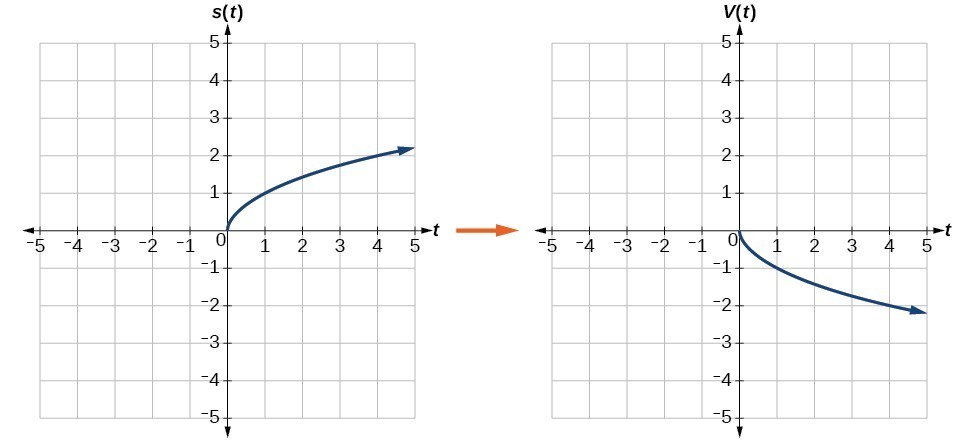



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra
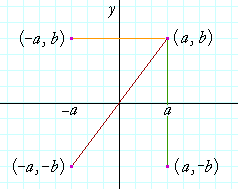



Reflections Of A Graph Topics In Precalculus



1




How To Reflect A Graph Through The X Axis Studypug




Graphing Reflecting Functions Study Com



Transformations Ib Math Stuff




What Is The Equation Of This Function After It Is Reflected Over The X Axis Brainly Com
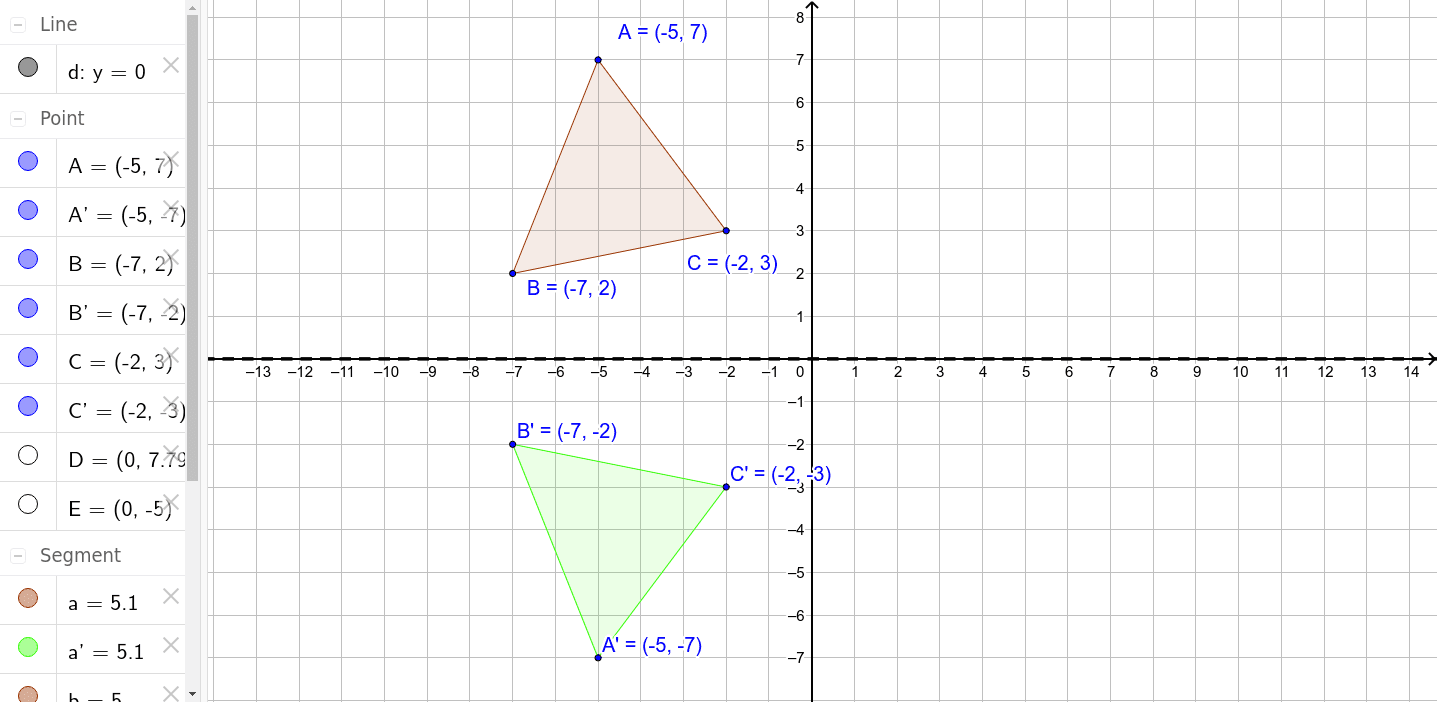



Reflection Over X Axis Geogebra




What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic
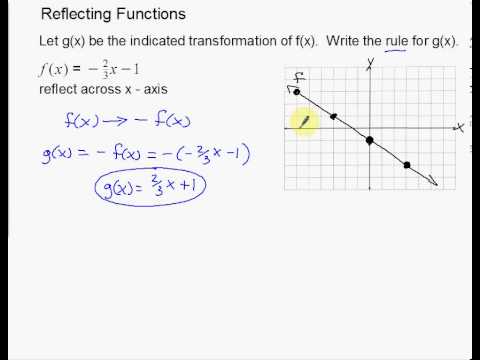



Linear Reflections Across X And Y Axis Example Youtube




How To Reflect Quadratic Equations Video Lesson Transcript Study Com




What Is The Equation Of This Function After Is Reflected Over The X Axis A F X 3 X 2 3 B Brainly Com
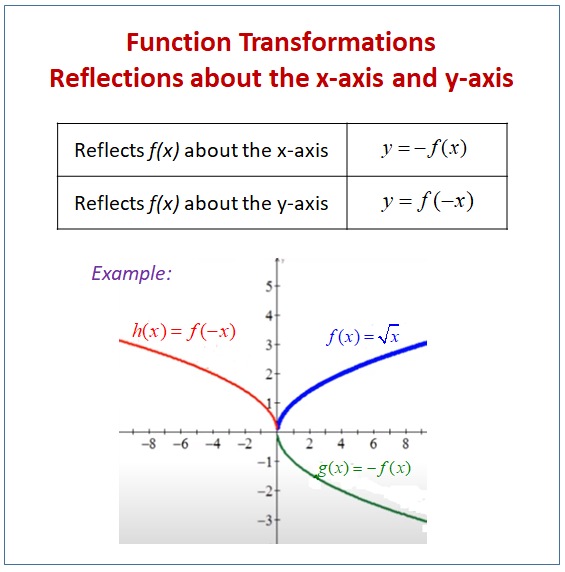



Reflecting Functions Or Graphs Examples Solutions Worksheets Videos Games Activities




Learn About Reflection Over The Line Y X Caddell Prep Online
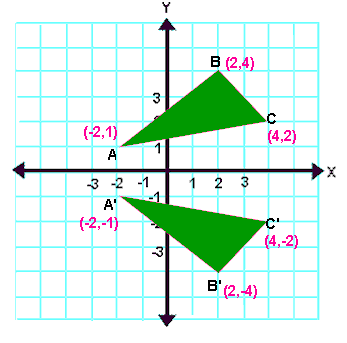



Reflection Transformation Matrix



A Review Of Logarithms
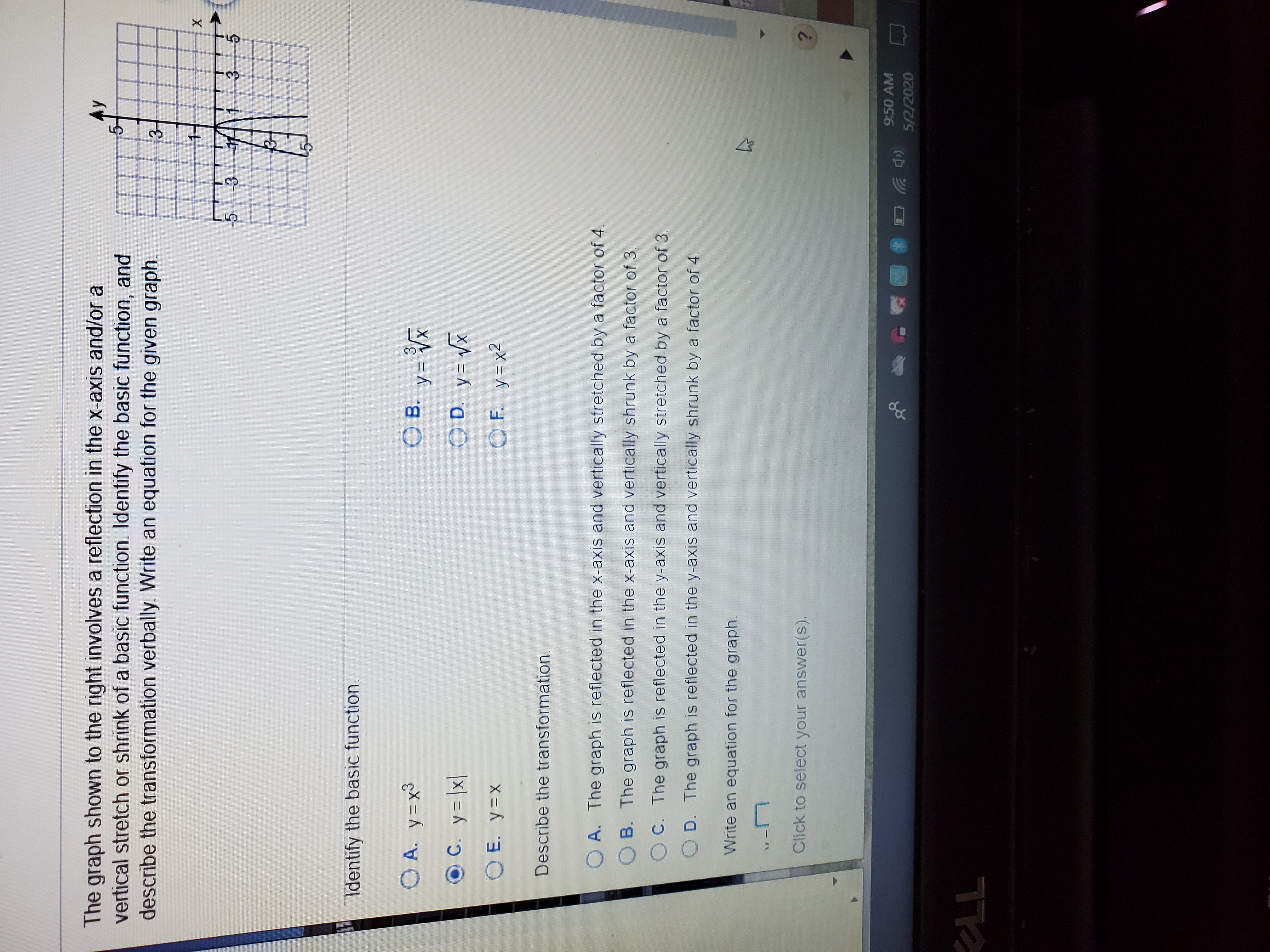



Answered The Graph Shown To The Right Involves A Bartleby
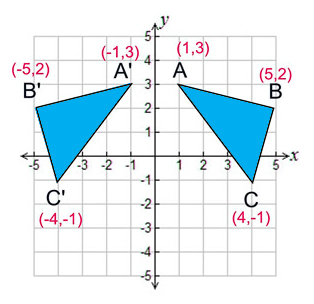



Reflection Definition Reflection In The Coordinate Plane




Pre Cal 40s Fall 06 Scribe Transformation




The Transformation Of The Graph Of A Quadratic Equation Matherudition




Content Transformations Of The Parabola



Discovering Advanced Algebra Resources
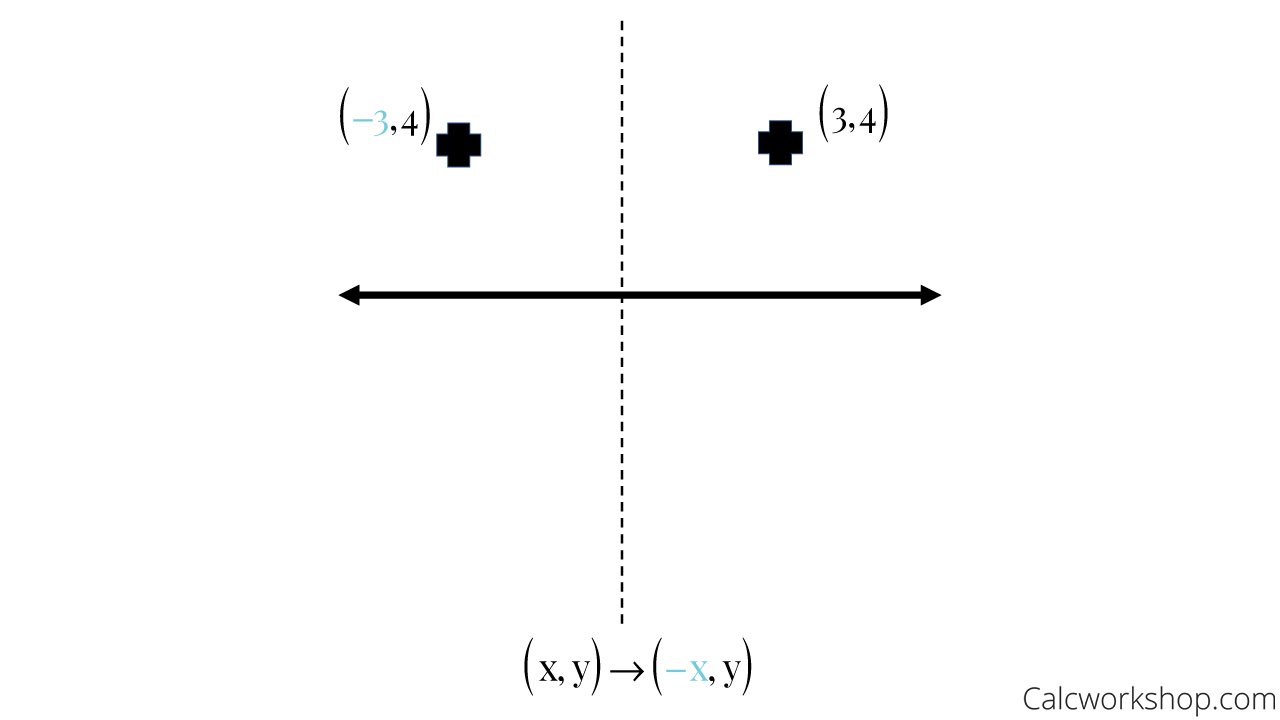



Reflection Rules How To W 25 Step By Step Examples
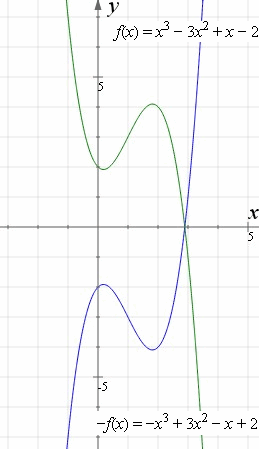



How To Reflect A Graph Through The X Axis Y Axis Or Origin
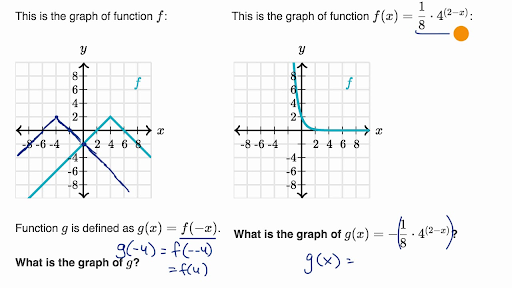



Reflecting Functions Examples Video Khan Academy




Content Transformations Of The Parabola




How To Reflect A Graph Through The X Axis Y Axis Or Origin
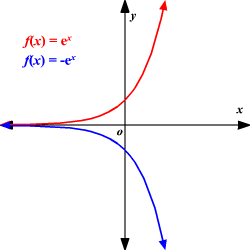



Transformation Of Function



0 件のコメント:
コメントを投稿